How to Read Confidence Interval Scatter Plot

Find definitions and interpretation guidance for every statistic and graph that is provided with the uncomplicated regression analysis.

95% CI

The confidence interval for the fit provides a range of likely values for the mean response given the specified settings of the predictors.

Interpretation

Apply the conviction interval to assess the estimate of the fitted value for the observed values of the variables.

For example, with a 95% confidence level, yous tin be 95% confident that the confidence interval contains the population mean for the specified values of the variables in the model. The confidence interval helps y'all appraise the practical significance of your results. Use your specialized knowledge to decide whether the confidence interval includes values that have applied significance for your state of affairs. A broad confidence interval indicates that you can be less confident about the mean of time to come values. If the interval is too wide to be useful, consider increasing your sample size.

95% PI

The prediction interval is a range that is probable to contain a single time to come response for a value of the predictor variable.

Interpretation

With 95% prediction bands, you can be 95% confident that new observations will autumn inside the interval indicated by the regal lines. (Notation, however, that this is merely truthful for density values that are within the range included in the assay.)

For example, a materials engineer at a furniture manufacturing site develops a simple regression model to predict the stiffness of particleboard from the density of the board. The engineer verifies that the model meets the assumptions of the analysis. Then, the annotator uses the model to predict the stiffness.

The regression equation predicts that the stiffness for a new observation with a density of 25 is -21.53 + 3.541*25, or 66.995. While it is unlikely that such an observation would take a stiffness of exactly 66.995, the prediction interval indicates that the engineer can be 95% confident that the actual value will be between approximately 48 and 86.

The prediction interval is always wider than the corresponding conviction interval. In this example, the 95% conviction interval indicates that the engineer can be 95% confident that the hateful stiffness will be between approximately 60 and 74.

Adj MS

Adjusted mean squares measure how much variation a term or a model explains, assuming that all other terms are in the model, regardless of the order they were entered. Unlike the adjusted sums of squares, the adjusted mean squares consider the degrees of freedom.

The adjusted mean square of the fault (too chosen MSE or due south²) is the variance effectually the fitted values.

Interpretation

Minitab uses the adjusted mean squares to calculate the p-value for a term. Minitab besides uses the adapted mean squares to calculate the adjusted R² statistic. Usually, y'all interpret the p-values and the adjusted R^two statistic instead of the adjusted mean squares.

Adj SS

Adjusted sums of squares are measures of variation for different components of the model. The guild of the predictors in the model does not bear on the calculation of the adjusted sum of squares. In the Analysis of Variance table, Minitab separates the sums of squares into unlike components that describe the variation due to different sources.

Adj SS Regression

The regression sum of squares is the sum of the squared deviations of the fitted response values from the mean response value. It quantifies the corporeality of variation in the response information that is explained by the model.

Adj SS Term

The adapted sum of squares for a term is the increase in the regression sum of squares compared to a model with only the other terms. It quantifies the amount of variation in the response data that is explained by each term in the model.

Adj SS Error

The error sum of squares is the sum of the squared residuals. It quantifies the variation in the data that the predictors do not explain.

Adj SS Total

The full sum of squares is the sum of the regression sum of squares and the error sum of squares. It quantifies the total variation in the data.

Estimation

Minitab uses the adapted sums of squares to summate the p-value for a term. Minitab also uses the sums of squares to summate the R² statistic. Ordinarily, you translate the p-values and the R² statistic instead of the sums of squares.

Coef

A regression coefficient describes the size and direction of the relationship between a predictor and the response variable. Coefficients are the numbers by which the values of the term are multiplied in a regression equation.

Estimation

The coefficient of the term represents the change in the mean response for a 1-unit modify in that term. The sign of the coefficient indicates the direction of the relationship betwixt the term and the response. If the coefficient is negative, as the term increases, the mean value of the response decreases. If the coefficient is positive, as the term increases, the hateful value of the response increases.

For example, a director determines that an employee's score on a job skills test can be predicted using the regression model y = 130 + 4.3x. In the equation, ten is the hours of in-firm training (from 0 to 20) and y is the test score. The coefficient, or slope, is 4.3, which indicates that, for every hour of training, the exam score increases, on average, by four.3 points.

The size of the coefficient is usually a expert fashion to evaluate the applied significance of the effect that a term has on the response variable. Still, the size of the coefficient does not indicate whether a term is statistically significant considering the calculations for significance also consider the variation in the response data. To determine statistical significance, examine the p-value for the term.

DF

The total degrees of liberty (DF) are the amount of information in your data. The analysis uses that information to estimate the values of unknown population parameters. The total DF is determined past the number of observations in your sample. The DF for a term show how much information that term uses. Increasing your sample size provides more data near the population, which increases the total DF. Increasing the number of terms in your model uses more information, which decreases the DF available to estimate the variability of the parameter estimates.

If two conditions are met, then Minitab partitions the DF for fault. The commencement condition is that there must be terms you lot can fit with the information that are not included in the electric current model. For example, if y'all have a continuous predictor with 3 or more singled-out values, you lot can estimate a quadratic term for that predictor. If the model does not include the quadratic term, then a term that the data tin fit is not included in the model and this status is met.

The second condition is that the data contain replicates. Replicates are observations where each predictor has the aforementioned value. For case, if yous accept 3 observations where pressure level is 5 and temperature is 25, then those 3 observations are replicates.

If the two conditions are met, then the 2 parts of the DF for error are lack-of-fit and pure error. The DF for lack-of-fit allow a exam of whether the model form is adequate. The lack-of-fit exam uses the degrees of freedom for lack-of-fit. The more DF for pure error, the greater the power of the lack-of-fit examination.

Fit

Fitted values are too called fits or 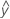. The fitted values are point estimates of the mean response for given values of the predictors. The values of the predictors are also called x-values.

Estimation

Fitted values are calculated by entering the specific 10-values for each observation in the data set into the model equation.

For instance, if the equation is y = 5 + 10x, the fitted value for the ten-value, 2, is 25 (25 = five + ten(two)).

Observations with fitted values that are very different from the observed value may be unusual. Observations with unusual predictor values may exist influential. If Minitab determines that your data include unusual or influential values, your output includes the table of Fits and Diagnostics for Unusual Observations, which identifies these observations. The unusual observations that Minitab labels exercise non follow the proposed regression equation well. Yet, it is expected that yous will have some unusual observations. For example, based on the criteria for large standardized residuals, you would look roughly 5% of your observations to be flagged every bit having a large standardized residual. For more information on unusual values, become to Unusual observations.

Fitted line plot

The fitted line plot displays the response and predictor data. The plot includes the regression line, which represents the regression equation. You can also choose to brandish the 95% confidence and prediction intervals on the plot.

Interpretation

Evaluate how well the model fits your data and whether the model meets your goals. Examine the fitted line plot to make up one's mind whether the following criteria are met:

• The sample contains an adequate number of observations throughout the entire range of all the predictor values.
• The model properly fits whatsoever curvature in the data. If you fit a linear model and run across curvature in the information, repeat the analysis and select the quadratic or cubic model. To determine which model is all-time, examine the plot and the goodness-of-fit statistics. Check the p-value for the terms in the model to make certain they are statistically significant, and apply process knowledge to evaluate applied significance.
• Await for any outliers, which can have a strong effect on the results. Try to identify the cause of any outliers. Right any data entry or measurement errors. Consider removing data values that are associated with abnormal, 1-fourth dimension events (special causes). And then, repeat the analysis. For more than information on detecting outliers, go to Unusual observations.

F-value

An F-value appears for each term in the Analysis of Variance table:

F-value for the model or the terms

The F-value is the test statistic used to determine whether the term is associated with the response.

F-value for the lack-of-fit examination

The F-value is the test statistic used to determine whether the model is missing higher-order terms that include the predictors in the current model.

Interpretation

Minitab uses the F-value to calculate the p-value, which you use to make a determination near the statistical significance of the terms and model. The p-value is a probability that measures the testify confronting the nil hypothesis. Lower probabilities provide stronger evidence against the zip hypothesis.

A sufficiently large F-value indicates that the term or model is pregnant.

If yous desire to use the F-value to determine whether to reject the zero hypothesis, compare the F-value to your critical value. Y'all tin calculate the disquisitional value in Minitab or find the critical value from an F-distribution tabular array in most statistics books. For more information on using Minitab to calculate the critical value, go to Using the inverse cumulative distribution function (ICDF) and click "Employ the ICDF to calculate critical values".

Histogram of residuals

The histogram of the residuals shows the distribution of the residuals for all observations.

Interpretation

Use the histogram of the residuals to determine whether the information are skewed or include outliers. The patterns in the following table may betoken that the model does not run across the model assumptions.

Pattern	What the pattern may point
A long tail in one direction	Skewness
A bar that is far abroad from the other bars	An outlier

Because the appearance of a histogram depends on the number of intervals used to grouping the data, don't employ a histogram to assess the normality of the residuals. Instead, use a normal probability plot.

A histogram is most effective when you lot have approximately 20 or more information points. If the sample is too pocket-size, so each bar on the histogram does non contain enough data points to reliably show skewness or outliers.

Normal probability plot of the residuals

The normal plot of the residuals displays the residuals versus their expected values when the distribution is normal.

Estimation

Use the normal probability plot of residuals to verify the assumption that the residuals are normally distributed. The normal probability plot of the residuals should approximately follow a straight line.

The following patterns violate the assumption that the residuals are normally distributed.

Southward-curve implies a distribution with long tails.

Inverted S-curve implies a distribution with short tails.

Downward bend implies a right-skewed distribution.

A few points lying away from the line implies a distribution with outliers.

If you encounter a nonnormal pattern, utilize the other residual plots to cheque for other bug with the model, such as missing terms or a fourth dimension club issue. If the residuals practice non follow a normal distribution, prediction intervals can be inaccurate. If the residuals do not follow a normal distribution and the information have fewer than 15 observations, and so confidence intervals for predictions, confidence intervals for coefficients, and p-values for coefficients can be inaccurate.

P-value – Lack-of-fit

The p-value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger evidence confronting the zero hypothesis.

Interpretation

To determine whether the model correctly specifies the relationship betwixt the response and the predictors, compare the p-value for the lack-of-fit test to your significance level to appraise the zippo hypothesis. The cypher hypothesis for the lack-of-fit exam is that the model correctly specifies the relationship between the response and the predictors. Usually, a significance level (denoted as alpha or α) of 0.05 works well. A significance level of 0.05 indicates a five% hazard of concluding that the model correctly specifies the relationship between the response and the predictors when the model does non.

P-value ≤ α: The lack-of-fit is statistically significant

If the p-value is less than or equal to the significance level, y'all conclude that the model does not correctly specify the relationship. To improve the model, you may need to add together terms or transform your data.

P-value > α: The lack-of-fit is not statistically pregnant

If the p-value is larger than the significance level, the test does non detect whatsoever lack-of-fit.

P-value – Regression

The p-value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger prove against the null hypothesis.

Estimation

To determine whether the model explains the variation in the response, compare the p-value for the model to your significance level to appraise the null hypothesis. The zippo hypothesis for the overall regression is that the model does not explain any of the variation in the response. Usually, a significance level (denoted as α or alpha) of 0.05 works well. A significance level of 0.05 indicates a five% risk of terminal that the model explains variation in the response when the model does not.

P-value ≤ α: The model explains variation in the response

If the p-value is less than or equal to the significance level, you conclude that the model explains variation in the response.

P-value > α: There is not enough evidence to conclude that the model explains variation in the response

If the p-value is greater than the significance level, you lot cannot conclude that the model explains variation in the response. You may want to fit a new model.

P-value – Term

The p-value is a probability that measures the evidence against the zero hypothesis. Lower probabilities provide stronger evidence against the nil hypothesis.

Estimation

To determine whether the association between the response and each term in the model is statistically significant, compare the p-value for the term to your significance level to assess the cipher hypothesis. The zero hypothesis is that the term's coefficient is equal to nothing, which indicates that there is no clan betwixt the term and the response. Usually, a significance level (denoted as α or blastoff) of 0.05 works well. A significance level of 0.05 indicates a 5% risk of concluding that an association exists when in that location is no bodily association.

P-value ≤ α: The association is statistically pregnant

If the p-value is less than or equal to the significance level, you tin can conclude that there is a statistically significant association between the response variable and the term.

P-value > α: The association is not statistically significant

If the p-value is greater than the significance level, you cannot conclude that there is a statistically significant association between the response variable and the term. If you fit a quadratic model or a cubic model and the quadratic or cubic terms are non statistically meaning, you may want to select a unlike model.

R-sq

R² is the percentage of variation in the response that is explained by the model. It is calculated as 1 minus the ratio of the error sum of squares (which is the variation that is not explained by model) to the total sum of squares (which is the full variation in the model).

Interpretation

Utilise R² to decide how well the model fits your data. The higher the R² value, the meliorate the model fits your data. R² is always betwixt 0% and 100%.

Y'all tin use a fitted line plot to graphically illustrate different R² values. The first plot illustrates a simple regression model that explains 85.v% of the variation in the response. The second plot illustrates a model that explains 22.vi% of the variation in the response. The more than variation that is explained by the model, the closer the data points autumn to the fitted regression line. Theoretically, if a model could explain 100% of the variation, the fitted values would always equal the observed values and all of the data points would fall on the fitted line.

Consider the following bug when interpreting the Rⁱⁱ value:

• R² ever increases when y'all add boosted predictors to a model. For case, the best 5-predictor model volition always have an R^two that is at least as high the best four-predictor model. Therefore, R² is virtually useful when you compare models of the aforementioned size.

• Small samples do non provide a precise estimate of the forcefulness of the human relationship between the response and predictors. If yous need R² to be more precise, yous should use a larger sample (typically, 40 or more).

• R^two is just one mensurate of how well the model fits the data. Fifty-fifty when a model has a loftier R², y'all should check the balance plots to verify that the model meets the model assumptions.

R-sq (adj)

Adjusted R² is the percentage of the variation in the response that is explained by the model, adapted for the number of predictors in the model relative to the number of observations. Adapted R² is calculated every bit 1 minus the ratio of the mean square error (MSE) to the hateful square total (MS Full).

Estimation

Use adjusted R² when you want to compare models that accept different numbers of predictors. R² ever increases when yous add a predictor to the model, even when in that location is no real comeback to the model. The adjusted R^two value incorporates the number of predictors in the model to assistance you choose the correct model.

For example, you lot work for a potato chip company that examines the factors that touch on the percent of crumbled potato chips per container. You receive the post-obit results every bit you add the predictors in a forward stepwise approach:

Footstep	% Irish potato	Cooling rate	Cooking temp	R2	Adapted Rtwo	P-value
1	10			52%	51%	0.000
2	X	X		63%	62%	0.000
3	X	10	X	65%	62%	0.000

The kickoff step yields a statistically significant regression model. The second footstep adds cooling rate to the model. Adjusted R² increases, which indicates that cooling rate improves the model. The third stride, which adds cooking temperature to the model, increases the R² but non the adapted R². These results signal that cooking temperature does non improve the model. Based on these results, y'all consider removing cooking temperature from the model.

R-sq (pred)

Predicted R² is calculated with a formula that is equivalent to systematically removing each ascertainment from the data set, estimating the regression equation, and determining how well the model predicts the removed observation. The value of predicted R² ranges between 0% and 100%. (While the calculations for predicted R² tin produce negative values, Minitab displays zero for these cases.)

Interpretation

Utilize predicted R² to decide how well your model predicts the response for new observations. Models that have larger predicted Rⁱⁱ values accept better predictive ability.

A predicted R² that is essentially less than R² may point that the model is over-fit. An over-fit model occurs when yous add together terms for effects that are non important in the population, although they may announced important in the sample data. The model becomes tailored to the sample data and therefore, may non exist useful for making predictions about the population.

Predicted Rⁱⁱ can besides be more useful than adjusted R² for comparing models because it is calculated with observations that are not included in the model calculation.

For example, an analyst at a financial consulting visitor develops a model to predict future market weather. The model looks promising because it has an R² of 87%. However, the predicted R^two is but to 52%, which indicates that the model may be over-fit.

Regression equation

Use the regression equation to describe the relationship between the response and the terms in the model. The regression equation is an algebraic representation of the regression line. The regression equation for the linear model takes the post-obit form: y = b₀ + b₁ten₁. In the regression equation, y is the response variable, b₀ is the abiding or intercept, b_one is the estimated coefficient for the linear term (also known as the slope of the line), and x₁ is the value of the term.

The regression equation with more than one term takes the post-obit form:

y = b₀ + b₁x₁ + b₂x₂ + ... + b_kx_k

In the regression equation, the letters correspond the following:

• y is the response variable
• b₀ is the constant
• b_one, b_two, ..., b_chiliad are the coefficients
• x₁, x₂, ..., 10_k are the values of the term

Resid

A residual (e_i) is the departure between an observed value (y) and the corresponding fitted value, ( 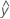), which is the value predicted by the model.

This scatterplot displays the weight versus the peak for a sample of adult males. The fitted regression line represents the relationship between tiptop and weight. If the height equals 6 feet, the fitted value for weight is 190 pounds. If the actual weight is 200 pounds, the remainder is x.

Interpretation

Plot the residuals to make up one's mind whether your model is adequate and meets the assumptions of regression. Examining the residuals can provide useful data almost how well the model fits the data. In general, the residuals should exist randomly distributed with no obvious patterns and no unusual values. If Minitab determines that your data include unusual observations, information technology identifies those observations in the Fits and Diagnostics for Unusual Observations tabular array in the output. The observations that Minitab labels as unusual practice not follow the proposed regression equation well. However, it is expected that you will take some unusual observations. For example, based on the criteria for large residuals, you would expect roughly 5% of your observations to be flagged as having a large rest. For more than data on unusual values, go to Unusual observations.

Residuals versus fits

The residuals versus fits graph plots the residuals on the y-axis and the fitted values on the ten-axis.

Interpretation

Employ the residuals versus fits plot to verify the assumption that the residuals are randomly distributed and take abiding variance. Ideally, the points should fall randomly on both sides of 0, with no recognizable patterns in the points.

The patterns in the post-obit tabular array may indicate that the model does not meet the model assumptions.

Blueprint	What the pattern may signal
Fanning or uneven spreading of residuals across fitted values	Nonconstant variance
Curvilinear	A missing higher-order term
A point that is far away from zero	An outlier
A betoken that is far away from the other points in the x-direction	An influential point

The post-obit graphs show an outlier and a violation of the assumption that the residuals are constant.

Plot with outlier

Ane of the points is much larger than all of the other points. Therefore, the betoken is an outlier. If at that place are too many outliers, the model may non be adequate. You should effort to place the cause of whatsoever outlier. Correct any data entry or measurement errors. Consider removing information values that are associated with aberrant, one-time events (special causes). And then, repeat the analysis.

Plot with nonconstant variance

The variance of the residuals increases with the fitted values. Find that, every bit the value of the fits increases, the scatter amidst the residuals widens. This pattern indicates that the variances of the residuals are unequal (nonconstant).

If you lot identify any patterns or outliers in your rest versus fits plot, consider the following solutions:

Issue	Possible solution
Nonconstant variance	Transform the response variable. You tin transform the variable in Minitab Statistical Software.
An outlier or influential bespeak	Verify that the observation is non a measurement error or data-entry error. Consider performing the analysis without this observation to make up one's mind how it impacts your results.
A missing higher-social club term	Add together the term and refit the model.

Residuals versus society

The remainder versus order plot displays the residuals in the guild that the information were collected.

Interpretation

Use the residuals versus order plot to verify the assumption that the residuals are contained from one some other. Independent residuals show no trends or patterns when displayed in time order. Patterns in the points may indicate that residuals near each other may be correlated, and thus, not independent. Ideally, the residuals on the plot should fall randomly effectually the center line:

Residuals versus variables

The residuals versus variables plot displays the residuals versus some other variable. The variable could already be included in your model. Or, the variable may not be in the model, but yous doubtable it affects the response.

Interpretation

If the variable is already included in the model, use the plot to determine whether you should add a higher-order term of the variable. If the variable is not already included in the model, use the plot to decide whether the variable is affecting the response in a systematic manner.

These patterns can identify an important variable or term.

Pattern	What the design may indicate
Pattern in residuals	The variable affects the response in a systematic way. If the variable is not in your model, include a term for that variable and refit the model.
Curvature in the points	A college-society term of the variable should be included in the model. For example, a curved blueprint indicates that y'all should add a squared term.

S

S represents how far the data values fall from the fitted values. Southward is measured in the units of the response.

Interpretation

Use Due south to assess how well the model describes the response. South is measured in the units of the response variable and represents the how far the data values fall from the fitted values. The lower the value of S, the improve the model describes the response. Yet, a low S value past itself does non bespeak that the model meets the model assumptions. Yous should check the residual plots to verify the assumptions.

For example, you work for a potato chip company that examines the factors that affect the percentage of crumbled potato chips per container. You reduce the model to the significant predictors, and Southward is calculated every bit 1.79. This result indicates that the standard deviation of the information points effectually the fitted values is 1.79. If you are comparison models, values that are lower than 1.79 indicate a ameliorate fit, and higher values indicate a worse fit.

SE Coef

The standard error of the coefficient estimates the variability betwixt coefficient estimates that you lot would obtain if you took samples from the same population once more and again.

Interpretation

Use the standard mistake of the coefficient to measure the precision of the estimate of the coefficient. The smaller the standard error, the more precise the guess. Dividing the coefficient by its standard error calculates a t-value. If the p-value associated with this t-statistic is less than your significance level (denoted equally blastoff or α), yous conclude that the coefficient is statistically significant.

For example, technicians judge a model for insolation as part of a solar thermal energy exam:

Coefficients Term Coef SE Coef T-Value P-Value VIF Constant 809 377 ii.14 0.042 South 20.81 8.65 2.41 0.024 ii.24 Due north -23.7 17.4 -1.36 0.186 2.17 Time of Solar day -thirty.2 x.8 -2.79 0.010 three.86

In this model, N and South measure the position of a focal point in inches. The coefficients for N and South are similar in magnitude. The standard error of the Southward coefficient is smaller than that of North. Therefore, the model is able to judge the coefficient for South with greater precision.

The standard fault of the Due north coefficient is about equally large as the value of the coefficient itself. The resulting p-value is greater than common levels of the significance level, so you cannot conclude that the coefficient for North differs from 0.

While the coefficient for South is closer to 0 than the coefficient for North, the standard error of the coefficient for South is as well smaller. The resulting p-value is smaller than mutual significance levels. Because the estimate of the coefficient for South is more precise, y'all can conclude that the coefficient for S differs from 0.

Statistical significance is one criterion you tin use to reduce a model in multiple regression. For more information, go to Model reduction.

Std Resid

The standardized residue equals the value of a remainder (e_i) divided past an estimate of its standard deviation.

Estimation

Use the standardized residuals to help you discover outliers. Standardized residuals greater than 2 and less than −2 are usually considered large. The Fits and Diagnostics for Unusual Observations table identifies these observations with an 'R'. The observations that Minitab labels do non follow the proposed regression equation well. However, information technology is expected that you will take some unusual observations. For instance, based on the criteria for large standardized residuals, you would look roughly five% of your observations to exist flagged as having a big standardized residual. For more information, go to Unusual observations.

Standardized residuals are useful because raw residuals might not be good indicators of outliers. The variance of each raw residue can differ by the x-values associated with it. This unequal variation causes it to be difficult to appraise the magnitudes of the raw residuals. Standardizing the residuals solves this problem by converting the different variances to a common scale.

T-value

The t-value measures the ratio betwixt the coefficient and its standard error.

Interpretation

Minitab uses the t-value to calculate the p-value, which you use to examination whether the coefficient is significantly dissimilar from 0.

Y'all tin can employ the t-value to determine whether to reject the null hypothesis. However, the p-value is used more often considering the threshold for the rejection of the null hypothesis does not depend on the degrees of freedom. For more information on using the t-value, go to Using the t-value to determine whether to reject the null hypothesis.

VIF

The variance inflation factor (VIF) indicates how much the variance of a coefficient is inflated due to the correlations among the predictors in the model.

Interpretation

Utilise the VIF to draw how much multicollinearity (which is correlation between predictors) exists in a regression analysis. Multicollinearity is problematic because it tin increment the variance of the regression coefficients, making it difficult to evaluate the individual touch on that each of the correlated predictors has on the response.

Use the following guidelines to interpret the VIF:

VIF	Status of predictors
VIF = 1	Non correlated
i < VIF < five	Moderately correlated
VIF > v	Highly correlated

VIF values greater than 5 propose that the regression coefficients are poorly estimated due to astringent multicollinearity.

For more data on multicollinearity and how to mitigate the effects of multicollinearity, run into Multicollinearity in regression.

buttshisfier.blogspot.com

Source: https://support.minitab.com/en-us/minitab-express/1/help-and-how-to/modeling-statistics/regression/how-to/simple-regression/interpret-the-results/all-statistics-and-graphs/

Share this post